3-1 Accuracy(정확도) // 2진분류면 잘 사용안함 (정상&비정상//남성여성)
분류 성능 평가지표 - 정확도, 오차행렬, 정밀도, 재현율, F1스코어, ROC AUC
import numpy as np
from sklearn.base import BaseEstimator
class MyDummyClassifier(BaseEstimator):
# fit( ) 메소드는 아무것도 학습하지 않음.
def fit(self, X , y=None):
pass
# predict( ) 메소드는 단순히 Sex feature가 1 이면 0 , 그렇지 않으면 1 로 예측함.
def predict(self, X):
pred = np.zeros( ( X.shape[0], 1 ))
for i in range (X.shape[0]) :
if X['Sex'].iloc[i] == 1:
pred[i] = 0
else :
pred[i] = 1
return pred
import pandas as pd
from sklearn.preprocessing import LabelEncoder
# Null 처리 함수
def fillna(df):
df['Age'].fillna(df['Age'].mean(),inplace=True)
df['Cabin'].fillna('N',inplace=True)
df['Embarked'].fillna('N',inplace=True)
df['Fare'].fillna(0,inplace=True)
return df
# 머신러닝 알고리즘에 불필요한 속성 제거
def drop_features(df):
df.drop(['PassengerId','Name','Ticket'],axis=1,inplace=True)
return df
# 레이블 인코딩 수행.
def format_features(df):
df['Cabin'] = df['Cabin'].str[:1]
features = ['Cabin','Sex','Embarked']
for feature in features:
le = LabelEncoder()
le = le.fit(df[feature])
df[feature] = le.transform(df[feature])
return df
# 앞에서 설정한 Data Preprocessing 함수 호출
def transform_features(df):
df = fillna(df)
df = drop_features(df)
df = format_features(df)
return df
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할.
titanic_df = pd.read_csv('./titanic_train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test=train_test_split(X_titanic_df, y_titanic_df, \
test_size=0.2, random_state=0)
# 위에서 생성한 Dummy Classifier를 이용하여 학습/예측/평가 수행.
myclf = MyDummyClassifier()
myclf.fit(X_train ,y_train)
mypredictions = myclf.predict(X_test)
print('Dummy Classifier의 정확도는: {0:.4f}'.format(accuracy_score(y_test , mypredictions)))
# Dummy Classifier의 정확도는: 0.7877
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.base import BaseEstimator
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pd
class MyFakeClassifier(BaseEstimator):
def fit(self,X,y):
pass
# 입력값으로 들어오는 X 데이터 셋의 크기만큼 모두 0값으로 만들어서 반환
def predict(self,X):
return np.zeros( (len(X), 1) , dtype=bool)
# 사이킷런의 내장 데이터 셋인 load_digits( )를 이용하여 MNIST 데이터 로딩
digits = load_digits()
print(digits.data)
print("### digits.data.shape:", digits.data.shape)
print(digits.target)
print("### digits.target.shape:", digits.target.shape)
[[ 0. 0. 5. ... 0. 0. 0.]
[ 0. 0. 0. ... 10. 0. 0.]
[ 0. 0. 0. ... 16. 9. 0.]
...
[ 0. 0. 1. ... 6. 0. 0.]
[ 0. 0. 2. ... 12. 0. 0.]
[ 0. 0. 10. ... 12. 1. 0.]]
### digits.data.shape: (1797, 64)
[0 1 2 ... 8 9 8]
### digits.target.shape: (1797,)
digits.target == 7
# array([False, False, False, ..., False, False, False])
# digits번호가 7번이면 True이고 이를 astype(int)로 1로 변환, 7번이 아니면 False이고 0으로 변환.
y = (digits.target == 7).astype(int)
X_train, X_test, y_train, y_test = train_test_split( digits.data, y, random_state=11)
# 불균형한 레이블 데이터 분포도 확인.
print('레이블 테스트 세트 크기 :', y_test.shape)
print('테스트 세트 레이블 0 과 1의 분포도')
print(pd.Series(y_test).value_counts())
# Dummy Classifier로 학습/예측/정확도 평가
fakeclf = MyFakeClassifier()
fakeclf.fit(X_train , y_train)
fakepred = fakeclf.predict(X_test)
print('모든 예측을 0으로 하여도 정확도는:{:.3f}'.format(accuracy_score(y_test , fakepred)))
# 2진분류에서 정확도는 애매함# 2진분류에서 정확도는 애매함
# 레이블 테스트 세트 크기 : (450,)
# 테스트 세트 레이블 0 과 1의 분포도
# 0 405
# 1 45
# dtype: int64
# 모든 예측을 0으로 하여도 정확도는:0.900
Confusion Matrix
2진분류 예측오류가 얼마인지 4분면으로 predicted Class X actual class => negative & positive 예측기준 실제가 같은지
from sklearn.metrics import confusion_matrix
# 앞절의 예측 결과인 fakepred와 실제 결과인 y_test의 Confusion Matrix출력
confusion_matrix(y_test , fakepred)
# array([[405, 0],
# [ 45, 0]], dtype=int64)
정밀도(Precision) 과 재현율(Recall)
정밀도 = TP / (FP + TP) 예측기준, FP가 낮게 /// 재현율 = TP / (FN + TP) 실제기준, FN이 낮게
** MyFakeClassifier의 예측 결과로 정밀도와 재현율 측정**
from sklearn.metrics import accuracy_score, precision_score , recall_score
print("정밀도:", precision_score(y_test, fakepred))
print("재현율:", recall_score(y_test, fakepred))
# 정밀도: 0.0
# 재현율: 0.0
** 오차행렬, 정확도, 정밀도, 재현율을 한꺼번에 계산하는 LAMBDA함수 생성 ** 서로 붙어다니니깐
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
def get_clf_eval(y_test , pred):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy , precision ,recall))
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할.
titanic_df = pd.read_csv('./titanic_train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, \
test_size=0.20, random_state=11)
lr_clf = LogisticRegression()
lr_clf.fit(X_train , y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test , pred)
# 오차 행렬
# [[104 14]
# [ 13 48]]
# 정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869Precision/Recall Trade-off : 둘 중 하나는 포기해야 한다
정밀도(FP X)가 중요한 경우 : 익플 느슨방화벽, 물량빨을 거르는 채, 아닌 애(정상메일)neg를 pos로 하지 않는게 중요, 스팸메일 ///
재현율(FN X)이 중요한 경우 : 크롬 무한방화벽 쪽집개, 맞는애(암 발생)Pos를 neg로 하지 않는게 중요, 암진단, 금융사기판별 ///
불균형레이블클래스 경우 매우 적은 수 결과값에 Pos 설정 1부여
분류의 결정 임곗값(threshold) 조정, but trade off 임계값 별 정밀도, 재현율 조정
조정 방법 => 임계점 0.5이면 그 초과0.55는 0에 해당, 0.45는 1에 해당 => 줄다리기
** predict_proba( ) 메소드 확인 **
사이킷런 estimator객체의 predict_proba()메소드는 분류결정 예측확률을 반환 분류결정임곗값을 조정하면서 예측확률 변경할 수 있음
pred_proba = lr_clf.predict_proba(X_test)
pred = lr_clf.predict(X_test)
print('pred_proba()결과 Shape : {0}'.format(pred_proba.shape))
print('pred_proba array에서 앞 3개만 샘플로 추출 \n:', pred_proba[:3])
# 예측 확률 array 와 예측 결과값 array 를 concatenate 하여 예측 확률과 결과값을 한눈에 확인
pred_proba_result = np.concatenate([pred_proba , pred.reshape(-1,1)],axis=1)
print('두개의 class 중에서 더 큰 확률을 클래스 값으로 예측 \n',pred_proba_result[:3])
# pred는 1차원이기 때문에 reshape(-1, 1)2차원으로 바꿔줌
#첫번째 열이 0이 될 확률, 2번째 열이 1이 될 확률 // 임계값 몇일까??
pred_proba()결과 Shape : (179, 2)
pred_proba array에서 앞 3개만 샘플로 추출
: [[0.4616653 0.5383347 ]
[0.87862763 0.12137237]
[0.87727002 0.12272998]]
두개의 class 중에서 더 큰 확률을 클래스 값으로 예측
[[0.4616653 0.5383347 1. ]
[0.87862763 0.12137237 0. ]
[0.87727002 0.12272998 0. ]]
Binarizer 활용 **
from sklearn.preprocessing import Binarizer
X = [[ 1, -1, 2],
[ 2, 0, 0],
[ 0, 1.1, 1.2]]
# threshold (1.1) 기준값보다 같거나 작으면 0을, 크면 1을 반환
binarizer = Binarizer(threshold=1.1)
print(binarizer.fit_transform(X))
# [[0. 0. 1.]
# [1. 0. 0.]
# [0. 0. 1.]]
분류 결정 임계값 0.5 기반에서 Binarizer를 이용하여 예측값 변환
from sklearn.preprocessing import Binarizer
#Binarizer의 threshold 설정값. 분류 결정 임곗값임.
custom_threshold = 0.5
# predict_proba( ) 반환값의 두번째 컬럼 , 즉 Positive 클래스 컬럼 하나만 추출하여 Binarizer를 적용
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test, custom_predict)
# 오차 행렬
# [[104 14]
# [ 13 48]]
# 정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869
분류 결정 임계값 0.4 기반에서 Binarizer를 이용하여 예측값 변환 **
# Binarizer의 threshold 설정값을 0.4로 설정. 즉 분류 결정 임곗값을 0.5에서 0.4로 낮춤
custom_threshold = 0.4
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test , custom_predict)
# 오차 행렬
# [[99 19]
# [10 51]]
# 정확도: 0.8380, 정밀도: 0.7286, 재현율: 0.8361
여러개의 분류 결정 임곗값을 변경하면서 Binarizer를 이용하여 예측값 변환
# 테스트를 수행할 모든 임곗값을 리스트 객체로 저장.
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]
def get_eval_by_threshold(y_test , pred_proba_c1, thresholds):
# thresholds list객체내의 값을 차례로 iteration하면서 Evaluation 수행.
for custom_threshold in thresholds:
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
custom_predict = binarizer.transform(pred_proba_c1)
print('임곗값:',custom_threshold)
get_clf_eval(y_test , custom_predict)
get_eval_by_threshold(y_test ,pred_proba[:,1].reshape(-1,1), thresholds )
임곗값: 0.4
오차 행렬
[[99 19]
[10 51]]
정확도: 0.8380, 정밀도: 0.7286, 재현율: 0.8361
임곗값: 0.45
오차 행렬
[[103 15]
[ 12 49]]
정확도: 0.8492, 정밀도: 0.7656, 재현율: 0.8033
임곗값: 0.5
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869
임곗값: 0.55
오차 행렬
[[109 9]
[ 15 46]]
정확도: 0.8659, 정밀도: 0.8364, 재현율: 0.7541
임곗값: 0.6
오차 행렬
[[112 6]
[ 16 45]]
정확도: 0.8771, 정밀도: 0.8824, 재현율: 0.7377
precision_recall_curve( ) 를 이용하여 임곗값에 따른 정밀도-재현율 변화변화값 추출
from sklearn.metrics import precision_recall_curve
# 레이블 값이 1일때의 예측 확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
# 실제값 데이터 셋과 레이블 값이 1일 때의 예측 확률을 precision_recall_curve 인자로 입력
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1 )
print('반환된 분류 결정 임곗값 배열의 Shape:', thresholds.shape)
print('반환된 precisions 배열의 Shape:', precisions.shape)
print('반환된 recalls 배열의 Shape:', recalls.shape)
print("thresholds 5 sample:", thresholds[:5])
print("precisions 5 sample:", precisions[:5])
print("recalls 5 sample:", recalls[:5])
#반환된 임계값 배열 로우가 147건이므로 샘플로 10건만 추출하되, 임곗값을 15 Step으로 추출.
thr_index = np.arange(0, thresholds.shape[0], 15)
print('샘플 추출을 위한 임계값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값: ', np.round(thresholds[thr_index], 2))
# 15 step 단위로 추출된 임계값에 따른 정밀도와 재현율 값
print('샘플 임계값별 정밀도: ', np.round(precisions[thr_index], 3))
print('샘플 임계값별 재현율: ', np.round(recalls[thr_index], 3))
# 반환된 분류 결정 임곗값 배열의 Shape: (143,)
# 반환된 precisions 배열의 Shape: (144,)
# 반환된 recalls 배열의 Shape: (144,)
# thresholds 5 sample: [0.10393302 0.10393523 0.10395998 0.10735757 0.10891579]
# precisions 5 sample: [0.38853503 0.38461538 0.38709677 0.38961039 0.38562092]
# recalls 5 sample: [1. 0.98360656 0.98360656 0.98360656 0.96721311]
# 샘플 추출을 위한 임계값 배열의 index 10개: [ 0 15 30 45 60 75 90 105 120 135]
# 샘플용 10개의 임곗값: [0.1 0.12 0.14 0.19 0.28 0.4 0.57 0.67 0.82 0.95]
# 샘플 임계값별 정밀도: [0.389 0.44 0.466 0.539 0.647 0.729 0.836 0.949 0.958 1. ]
# 샘플 임계값별 재현율: [1. 0.967 0.902 0.902 0.902 0.836 0.754 0.607 0.377 0.148]
임곗값의 변경에 따른 정밀도-재현율 변화 곡선을 그림
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
def precision_recall_curve_plot(y_test , pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출.
precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
# X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
# threshold 값 X 축의 Scale을 0.1 단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )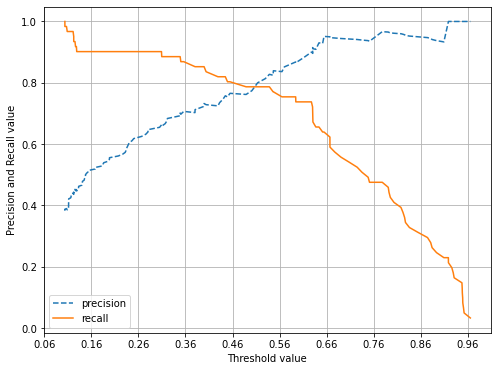
F1 Score
정밀도 100 => 확실한 경우만 pos // FP 줄이기 재현율 100 => 모든 경우를 pos // FN 줄이기 neg 0 지정 이 맹점을 보완하기 위해 f1-score 어느 한쪽에 치우치지 않을수록 높은 값 획득
from sklearn.metrics import f1_score
f1 = f1_score(y_test , pred)
print('F1 스코어: {0:.4f}'.format(f1))
F1 스코어: 0.7805
def get_clf_eval(y_test , pred):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
# F1 스코어 추가
f1 = f1_score(y_test,pred)
print('오차 행렬')
print(confusion)
# f1 score print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}, F1:{3:.4f}'.format(accuracy, precision, recall, f1))
thresholds = [0.4 , 0.45 , 0.50 , 0.55 , 0.60]
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test, pred_proba[:,1].reshape(-1,1), thresholds)
임곗값: 0.4
오차 행렬
[[99 19]
[10 51]]
정확도: 0.8380, 정밀도: 0.7286, 재현율: 0.8361, F1:0.7786
임곗값: 0.45
오차 행렬
[[103 15]
[ 12 49]]
정확도: 0.8492, 정밀도: 0.7656, 재현율: 0.8033, F1:0.7840
임곗값: 0.5
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869, F1:0.7805
임곗값: 0.55
오차 행렬
[[109 9]
[ 15 46]]
정확도: 0.8659, 정밀도: 0.8364, 재현율: 0.7541, F1:0.7931
임곗값: 0.6
오차 행렬
[[112 6]
[ 16 45]]
정확도: 0.8771, 정밀도: 0.8824, 재현율: 0.7377, F1:0.8036
ROC Curve와 AUC
Receiver Operation Characteristic Curve(무선통신장비 측정 툴)기반 AUC(Area Under Curve)값은 roc 곡선 면적으로 1에 가까울수록 좋은 수치 FPR(False Positive Rate)와 TPR(True Positive Rate) 관계 의학분야에 사용
from sklearn.metrics import roc_curve
# 레이블 값이 1일때의 예측 확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
fprs , tprs , thresholds = roc_curve(y_test, pred_proba_class1)
# 반환된 임곗값 배열 로우가 47건이므로 샘플로 10건만 추출하되, 임곗값을 5 Step으로 추출.
thr_index = np.arange(0, thresholds.shape[0], 5)
print('샘플 추출을 위한 임곗값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값: ', np.round(thresholds[thr_index], 2))
# 5 step 단위로 추출된 임계값에 따른 FPR, TPR 값
print('샘플 임곗값별 FPR: ', np.round(fprs[thr_index], 3))
print('샘플 임곗값별 TPR: ', np.round(tprs[thr_index], 3))
# 샘플 추출을 위한 임곗값 배열의 index 10개: [ 0 5 10 15 20 25 30 35 40 45 50]
# 샘플용 10개의 임곗값: [1.97 0.75 0.63 0.59 0.49 0.4 0.31 0.15 0.12 0.11 0.1 ]
# 샘플 임곗값별 FPR: [0. 0.017 0.034 0.059 0.127 0.161 0.237 0.483 0.61 0.703 0.814]
# 샘플 임곗값별 TPR: [0. 0.475 0.672 0.754 0.787 0.852 0.885 0.902 0.934 0.967 0.984]
def roc_curve_plot(y_test , pred_proba_c1):
# 임곗값에 따른 FPR, TPR 값을 반환 받음.
fprs , tprs , thresholds = roc_curve(y_test ,pred_proba_c1)
# ROC Curve를 plot 곡선으로 그림.
plt.plot(fprs , tprs, label='ROC')
# 가운데 대각선 직선을 그림.
plt.plot([0, 1], [0, 1], 'k--', label='Random')
# FPR X 축의 Scale을 0.1 단위로 변경, X,Y 축명 설정등
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
plt.xlim(0,1); plt.ylim(0,1)
plt.xlabel('FPR( 1 - Sensitivity )'); plt.ylabel('TPR( Recall )')
plt.legend()
plt.show()
roc_curve_plot(y_test, lr_clf.predict_proba(X_test)[:, 1] )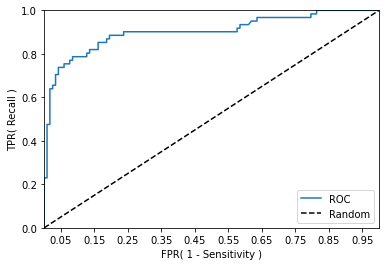
from sklearn.metrics import roc_auc_score
### 아래는 roc_auc_score()의 인자를 잘못 입력한 것으로, 책에서 수정이 필요한 부분입니다.
### 책에서는 roc_auc_score(y_test, pred)로 예측 타겟값을 입력하였으나
### roc_auc_score(y_test, y_score)로 y_score는 predict_proba()로 호출된 예측 확률 ndarray중 Positive 열에 해당하는 ndarray입니다.
#pred = lr_clf.predict(X_test)
#roc_score = roc_auc_score(y_test, pred)
pred_proba = lr_clf.predict_proba(X_test)[:, 1]
roc_score = roc_auc_score(y_test, pred_proba)
print('ROC AUC 값: {0:.4f}'.format(roc_score))
# ROC AUC 값: 0.9024
def get_clf_eval(y_test, pred=None, pred_proba=None):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
f1 = f1_score(y_test,pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
# ROC-AUC print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))
'Data_Science > ML_Perfect_Guide' 카테고리의 다른 글
| 4-1. iris || Decision Tree, GridSearchCV, feature importance, visualize_boundary (0) | 2021.12.22 |
|---|---|
| 3-2. Pima Indians Diabetes prediction (0) | 2021.12.22 |
| 2-5. titanic || sklearn (0) | 2021.12.22 |
| 2-4. Data Preprocessing (0) | 2021.12.22 |
| 2-3. model selection || sklearn (0) | 2021.12.22 |