728x90
반응형
# 시계열 데이터 : 연속적인 시간에 따라 다르게 측정데이터
# arima 모델 => statsmodel 모듈 이용
# ar 과거정보기준
# ma 이전정보의 오차를 현재 상태로 추론
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
file_path = 'market-price.csv'
bitcoin_df = pd.read_csv(file_path)
bitcoin_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 365 entries, 0 to 364
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Timestamp 365 non-null object
1 market-price 365 non-null float64
dtypes: float64(1), object(1)
memory usage: 5.8+ KB
bitcoin_df.head()
Timestamp market-price
0 2017-08-27 00:00:00 4354.308333
1 2017-08-28 00:00:00 4391.673517
2 2017-08-29 00:00:00 4607.985450
3 2017-08-30 00:00:00 4594.987850
4 2017-08-31 00:00:00 4748.255000
bitcoin_df = pd.read_csv('market-price.csv', names = ['day','price'], header=0)
bitcoin_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 365 entries, 0 to 364
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 day 365 non-null object
1 price 365 non-null float64
dtypes: float64(1), object(1)
memory usage: 5.8+ KB
bitcoin_df.head()
day price
0 2017-08-27 00:00:00 4354.308333
1 2017-08-28 00:00:00 4391.673517
2 2017-08-29 00:00:00 4607.985450
3 2017-08-30 00:00:00 4594.987850
4 2017-08-31 00:00:00 4748.255000
bitcoin_df.shape
# (365, 2)
bitcoin_df['day'] = pd.to_datetime(bitcoin_df['day'])
bitcoin_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 365 entries, 0 to 364
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 day 365 non-null datetime64[ns]
1 price 365 non-null float64
dtypes: datetime64[ns](1), float64(1)
memory usage: 5.8 KB
bitcoin_df.describe()
price
count 365.000000
mean 8395.863578
std 3239.804756
min 3319.630000
25% 6396.772500
50% 7685.633333
75% 9630.136277
max 19498.683333
bitcoin_df.plot()
plt.show()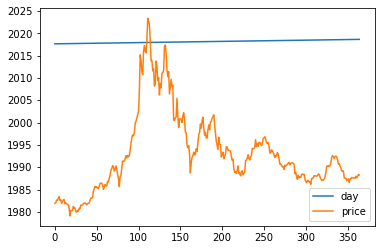
# arima 모델 학습
# order = (2,1,2)
# 2 => ar 2번째 과거까지 알고리즘에 넣음
# 1 => difference 차분 정보, 현재상태 - 바로 이전의 상태 뺀값
# 시계열 데이터의 불규칙성을 파악 => 비트코인 ^^
# 2 => ma 2번째 과거정보오차를 이용해서 현재를 추론
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(bitcoin_df.price.values, order=(2,1,2))
model_fit = model.fit(trend='c', full_output=True, disp=True)
fig = model_fit.plot_predict() # 학습 데이터에 대한 예측 결과 출력
risiduals = pd.DataFrame(model_fit.resid)# 잔차의 변동을 시각화
risiduals.plot()

# 실제데이터와 비교
# 이후 5일 정보 예측
forecast_data = model_fit.forecast(steps=5)
forecast_data
# 1 번 배열 : 예측값, 5일차 예측값
# 2 번 배열 : 표준오차, 5일차 예측값
# 3 번 배열 : 5개 배열 [예측데이터 하한값, 예측데이터 상한값]
(array([6676.91689529, 6685.04884511, 6690.29837254, 6697.35159419,
6703.26452567]),
array([ 512.41529746, 753.50414112, 914.97749885, 1061.45286959,
1184.4382798 ]),
array([[5672.60136715, 7681.23242343],
[5208.20786632, 8161.8898239 ],
[4896.97542813, 8483.62131695],
[4616.94219851, 8777.76098987],
[4381.80815535, 9024.720896 ]]))
# 실데이터 읽어오기
test_file_path = 'market-price-test.csv'
bitcoin_test_df = pd.read_csv(test_file_path, names = ['ds','y'], header=0)
# 예측값을 pred_y 변수에 리스트로 저장 // 원래 튜플
pred_y = forecast_data[0].tolist()
pred_y
[6676.9168952924865,
6685.048845109902,
6690.298372539306,
6697.35159419041,
6703.2645256732285]
# 실제값을 test_y 변수에 리스트로 저장하기
test_y = bitcoin_test_df['y'].values
test_y
pred_y_lower = [] # 최소 예측값
pred_y_upper = [] # 최대 예측값
for low_up in forecast_data[2] :
pred_y_lower.append(low_up[0])
pred_y_upper.append(low_up[1])
pred_y_lower
[5672.601367152579,
5208.207866318599,
4896.975428126821,
4616.942198505993,
4381.808155348637]
pred_y_upper
[7681.232423432394,
8161.889823901204,
8483.62131695179,
8777.760989874827,
9024.72089599782]
# 시각화
plt.plot(pred_y, color='gold') # 예측값
plt.plot(test_y, color='green') # 실제값 => 변동성있는 편
plt.plot(pred_y_lower, color='red') # 예측 최소값
plt.plot(pred_y_upper, color='blue') # 예측 최대값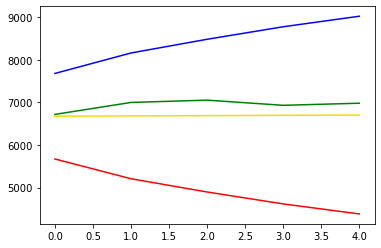
# 시계열 데이터 분석을 위한 모델
# ar (자기회귀분석모델)
그냥시간이 들어가서 연속적인 => 주가분석 등
현재 자신과 과거의 자신을 비교, 관계
ar(n) => n 이전의 시점
# ma 이동평균모델
과거와 현재의 오차의 관계
# 합쳐서 자기회귀 이동모델
arma(자기회귀 이동평균 모델)
현재시점의 나와 과거시점의 나를 비교
현재시점의 차이를 비교
# arima 자기회귀 누적 이동평균 모델
ma 누적차수 ar 누적차수 동시에
현재와 추세간의 관계 정의
arma는 규칙적인 시계열데이터는 가능하지만 불규칙적인 시계열에 불리, 한계
보완하기위한 모델이다
# arima(p, d, q)
p : ar 모형 차수
d : 차분 : 차이
q : ma 모형 차수
# p+q가 짝수인게 좋다
# 페이스북 시계열 알고리즘 prophet
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from fbprophet import Prophet
file_path = 'market-price.csv'
bitcoin_df = pd.read_csv(file_path, names = ['ds', 'y'], header=0)
bitcoin_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 365 entries, 0 to 364
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 ds 365 non-null object
1 y 365 non-null float64
dtypes: float64(1), object(1)
memory usage: 5.8+ KB
prophet = Prophet(seasonality_mode = 'multiplicative',
yearly_seasonality = True, # 연별
weekly_seasonality = True, # 주별
daily_seasonality = True, # 일별
changepoint_prior_scale = 0.5) # 과적합 방지 0.5만큼 만 분석
prophet.fit(bitcoin_df) # 학습하기pip install pystan --upgrade
# 5일 앞을 예측하기
future_data = prophet.make_future_dataframe(periods=5, freq='d')
# 예측
forecast_data = prophet.predict(future_data)
forecast_data
ds trend yhat_lower yhat_upper trend_lower trend_upper daily daily_lower daily_upper multiplicative_terms ... weekly weekly_lower weekly_upper yearly yearly_lower yearly_upper additive_terms additive_terms_lower additive_terms_upper yhat
0 2017-08-27 473.569120 3776.764014 5104.491150 473.569120 473.569120 9.563964 9.563964 9.563964 8.356854 ... -0.038472 -0.038472 -0.038472 -1.168637 -1.168637 -1.168637 0.0 0.0 0.0 4431.117317
1 2017-08-28 476.933144 3833.197375 5183.393019 476.933144 476.933144 9.563964 9.563964 9.563964 8.436224 ... -0.006602 -0.006602 -0.006602 -1.121138 -1.121138 -1.121138 0.0 0.0 0.0 4500.447825
2 2017-08-29 480.297167 3877.729283 5211.107968 480.297167 480.297167 9.563964 9.563964 9.563964 8.494301 ... 0.019974 0.019974 0.019974 -1.089637 -1.089637 -1.089637 0.0 0.0 0.0 4560.085805
3 2017-08-30 483.661190 3954.539662 5206.571586 483.661190 483.661190 9.563964 9.563964 9.563964 8.440425 ... -0.046634 -0.046634 -0.046634 -1.076905 -1.076905 -1.076905 0.0 0.0 0.0 4565.966993
4 2017-08-31 487.025213 3931.103385 5269.222802 487.025213 487.025213 9.563964 9.563964 9.563964 8.461194 ... -0.017649 -0.017649 -0.017649 -1.085122 -1.085122 -1.085122 0.0 0.0 0.0 4607.839822
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
365 2018-08-27 738.543896 6218.124910 7629.182104 738.543896 738.543896 9.563964 9.563964 9.563964 8.374726 ... -0.006602 -0.006602 -0.006602 -1.182636 -1.182636 -1.182636 0.0 0.0 0.0 6923.647020
366 2018-08-28 742.612648 6338.876532 7721.930490 742.612648 742.612648 9.563964 9.563964 9.563964 8.452304 ... 0.019974 0.019974 0.019974 -1.131634 -1.131634 -1.131634 0.0 0.0 0.0 7019.400574
367 2018-08-29 746.681400 6371.510730 7768.115586 746.681400 752.202325 9.563964 9.563964 9.563964 8.421478 ... -0.046634 -0.046634 -0.046634 -1.095851 -1.095851 -1.095851 0.0 0.0 0.0 7034.842537
368 2018-08-30 750.750152 6374.620387 7883.157582 748.285679 770.190606 9.563964 9.563964 9.563964 8.468117 ... -0.017649 -0.017649 -0.017649 -1.078198 -1.078198 -1.078198 0.0 0.0 0.0 7108.190099
369 2018-08-31 754.818904 6440.287682 7941.401382 742.825041 785.906885 9.563964 9.563964 9.563964 8.518827 ... 0.035872 0.035872 0.035872 -1.081008 -1.081008 -1.081008 0.0 0.0 0.0 7184.990775
370 rows × 22 columns
forecast_data.shape
# (370, 22)
# 예측된 데이터의 날짜 , 예측값, 최소 예측값, 최대 예측값
forecast_data[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail(5)
ds yhat yhat_lower yhat_upper
365 2018-08-27 6923.647020 6218.124910 7629.182104
366 2018-08-28 7019.400574 6338.876532 7721.930490
367 2018-08-29 7034.842537 6371.510730 7768.115586
368 2018-08-30 7108.190099 6374.620387 7883.157582
369 2018-08-31 7184.990775 6440.287682 7941.401382
# 결과 시각화
fig1 = prophet.plot(forecast_data)
# 검은점 : 실데이터
# 파란선 : 예측값
fig2 = prophet.plot_components(forecast_data)
# 4개의 데이터
# 원 데이터
# 주별
# 연별
# 시간별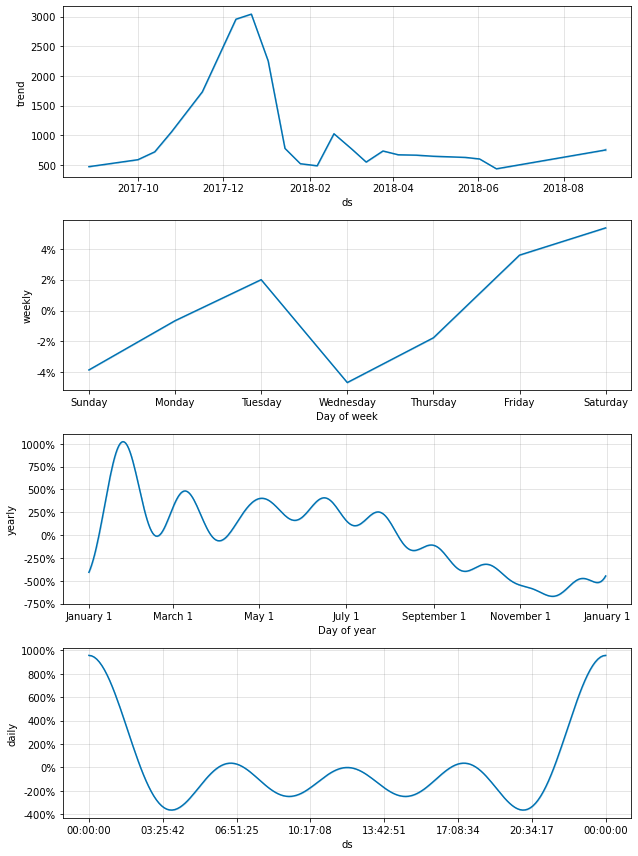
# 예측이니 성능 분석도 해야함
# 실제값 - 예측값
y = bitcoin_df.y.values[5:] # 실데이터, 첫5일제외,
y_pred = forecast_data.yhat.values[5:-5] #첫5일, 막5일 제외한 예측데이터
# r2score rmse
from sklearn.metrics import mean_squared_error, r2_score
from math import sqrt
r2 = r2_score(y, y_pred)
r2
# 0.9737786665877044
rmse = sqrt(mean_squared_error(y, y_pred))
rmse
# 522.2899311292591
# 실데이터와 비교
test_file_path = 'market-price-test.csv'
bitcoin_test_df = pd.read_csv(test_file_path, names = ['ds','y'], header=0)
bitcoin_test_df
ds y
0 2018-08-27 00:00:00 6719.266154
1 2018-08-28 00:00:00 7000.040000
2 2018-08-29 00:00:00 7054.276429
3 2018-08-30 00:00:00 6932.662500
4 2018-08-31 00:00:00 6981.946154
y = bitcoin_test_df.y.values
y
array([6719.26615385, 7000.04 , 7054.27642857, 6932.6625 ,
6981.94615385])
y_pred = forecast_data.yhat.values[-5:]
y_pred
array([6923.64702007, 7019.40057427, 7034.84253693, 7108.19009905,
7184.99077545])
plt.plot(y_pred, color = 'gold')
plt.plot(y, color = 'green')
반응형
'Data_Science > Data_Analysis_Py' 카테고리의 다른 글
| 30. 보스턴 주택가격정보 || 선형회귀 (0) | 2021.11.24 |
|---|---|
| 29. 비트코인 시계열 분석 || prophet (0) | 2021.11.24 |
| 27. 프로야구 연봉 예측 분석 || OLS, Heatmap (0) | 2021.11.24 |
| 26. 서울 중학교 졸업자 분석 || dbscan, folium (0) | 2021.11.24 |
| 25. 판매 데이터 분석 || kmeans (0) | 2021.11.24 |