728x90
반응형
Regularized Linear Model - Ridge Regression
# 앞의 LinearRegression예제에서 분할한 feature 데이터 셋인 X_data과 Target 데이터 셋인 Y_target 데이터셋을 그대로 이용
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
# boston 데이타셋 로드
boston = load_boston()
# boston 데이타셋 DataFrame 변환
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)
# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함.
bostonDF['PRICE'] = boston.target
print('Boston 데이타셋 크기 :',bostonDF.shape)
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
ridge = Ridge(alpha = 10)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 3))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores,3))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))
Boston 데이타셋 크기 : (506, 14)
5 folds 의 개별 Negative MSE scores: [-11.422 -24.294 -28.144 -74.599 -28.517]
5 folds 의 개별 RMSE scores : [3.38 4.929 5.305 8.637 5.34 ]
5 folds 의 평균 RMSE : 5.518
alpha값을 0 , 0.1 , 1 , 10 , 100 으로 변경하면서 RMSE 측정
# Ridge에 사용될 alpha 파라미터의 값들을 정의
alphas = [0 , 0.1 , 1 , 10 , 100]
# alphas list 값을 iteration하면서 alpha에 따른 평균 rmse 구함.
for alpha in alphas :
ridge = Ridge(alpha = alpha)
#cross_val_score를 이용하여 5 fold의 평균 RMSE 계산
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0} 일 때 5 folds 의 평균 RMSE : {1:.3f} '.format(alpha,avg_rmse))
alpha 0 일 때 5 folds 의 평균 RMSE : 5.829
alpha 0.1 일 때 5 folds 의 평균 RMSE : 5.788
alpha 1 일 때 5 folds 의 평균 RMSE : 5.653
alpha 10 일 때 5 folds 의 평균 RMSE : 5.518
alpha 100 일 때 5 folds 의 평균 RMSE : 5.330
각 alpha에 따른 회귀 계수 값을 시각화. 각 alpha값 별로 plt.subplots로 맷플롯립 축 생성
# 각 alpha에 따른 회귀 계수 값을 시각화하기 위해 5개의 열로 된 맷플롯립 축 생성
fig , axs = plt.subplots(figsize=(18,6) , nrows=1 , ncols=5)
# 각 alpha에 따른 회귀 계수 값을 데이터로 저장하기 위한 DataFrame 생성
coeff_df = pd.DataFrame()
# alphas 리스트 값을 차례로 입력해 회귀 계수 값 시각화 및 데이터 저장. pos는 axis의 위치 지정
for pos , alpha in enumerate(alphas) :
ridge = Ridge(alpha = alpha)
ridge.fit(X_data , y_target)
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=ridge.coef_ , index=X_data.columns )
colname='alpha:'+str(alpha)
coeff_df[colname] = coeff
# 막대 그래프로 각 alpha 값에서의 회귀 계수를 시각화. 회귀 계수값이 높은 순으로 표현
coeff = coeff.sort_values(ascending=False)
axs[pos].set_title(colname)
axs[pos].set_xlim(-3,6)
sns.barplot(x=coeff.values , y=coeff.index, ax=axs[pos])
# for 문 바깥에서 맷플롯립의 show 호출 및 alpha에 따른 피처별 회귀 계수를 DataFrame으로 표시
plt.show()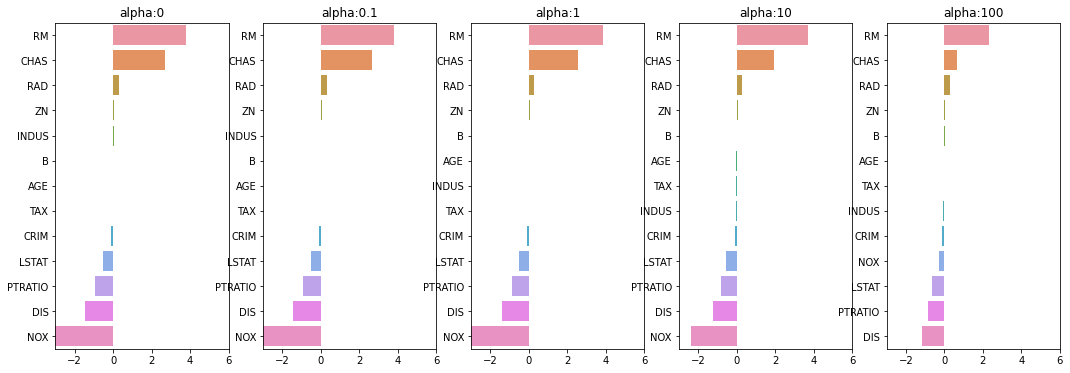
alpha 값에 따른 컬럼별 회귀계수 출력
ridge_alphas = [0 , 0.1 , 1 , 10 , 100]
sort_column = 'alpha:'+str(ridge_alphas[0])
coeff_df.sort_values(by=sort_column, ascending=False)
alpha:0 alpha:0.1 alpha:1 alpha:10 alpha:100
RM 3.809865 3.818233 3.854000 3.702272 2.334536
CHAS 2.686734 2.670019 2.552393 1.952021 0.638335
RAD 0.306049 0.303515 0.290142 0.279596 0.315358
ZN 0.046420 0.046572 0.047443 0.049579 0.054496
INDUS 0.020559 0.015999 -0.008805 -0.042962 -0.052826
B 0.009312 0.009368 0.009673 0.010037 0.009393
AGE 0.000692 -0.000269 -0.005415 -0.010707 0.001212
TAX -0.012335 -0.012421 -0.012912 -0.013993 -0.015856
CRIM -0.108011 -0.107474 -0.104595 -0.101435 -0.102202
LSTAT -0.524758 -0.525966 -0.533343 -0.559366 -0.660764
PTRATIO -0.952747 -0.940759 -0.876074 -0.797945 -0.829218
DIS -1.475567 -1.459626 -1.372654 -1.248808 -1.153390
NOX -17.766611 -16.684645 -10.777015 -2.371619 -0.262847
라쏘 회귀
from sklearn.linear_model import Lasso, ElasticNet
# alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None, verbose=True):
coeff_df = pd.DataFrame()
if verbose : print('####### ', model_name , '#######')
for param in params:
if model_name =='Ridge': model = Ridge(alpha=param)
elif model_name =='Lasso': model = Lasso(alpha=param)
elif model_name =='ElasticNet': model = ElasticNet(alpha=param, l1_ratio=0.7)
neg_mse_scores = cross_val_score(model, X_data_n,
y_target_n, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} '.format(param, avg_rmse))
# cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출
model.fit(X_data , y_target)
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=model.coef_ , index=X_data.columns )
colname='alpha:'+str(param)
coeff_df[colname] = coeff
return coeff_df
# end of get_linear_regre_eval
# 라쏘에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
lasso_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_lasso_df =get_linear_reg_eval('Lasso', params=lasso_alphas, X_data_n=X_data, y_target_n=y_target)
####### Lasso #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.612
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.615
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.669
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.776
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.189
# 반환된 coeff_lasso_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(lasso_alphas[0])
coeff_lasso_df.sort_values(by=sort_column, ascending=False)
alpha:0.07 alpha:0.1 alpha:0.5 alpha:1 alpha:3
RM 3.789725 3.703202 2.498212 0.949811 0.000000
CHAS 1.434343 0.955190 0.000000 0.000000 0.000000
RAD 0.270936 0.274707 0.277451 0.264206 0.061864
ZN 0.049059 0.049211 0.049544 0.049165 0.037231
B 0.010248 0.010249 0.009469 0.008247 0.006510
NOX -0.000000 -0.000000 -0.000000 -0.000000 0.000000
AGE -0.011706 -0.010037 0.003604 0.020910 0.042495
TAX -0.014290 -0.014570 -0.015442 -0.015212 -0.008602
INDUS -0.042120 -0.036619 -0.005253 -0.000000 -0.000000
CRIM -0.098193 -0.097894 -0.083289 -0.063437 -0.000000
LSTAT -0.560431 -0.568769 -0.656290 -0.761115 -0.807679
PTRATIO -0.765107 -0.770654 -0.758752 -0.722966 -0.265072
DIS -1.176583 -1.160538 -0.936605 -0.668790 -0.000000
엘라스틱넷 회귀
# 엘라스틱넷에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
# l1_ratio는 0.7로 고정
elastic_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_elastic_df =get_linear_reg_eval('ElasticNet', params=elastic_alphas,
X_data_n=X_data, y_target_n=y_target)
####### ElasticNet #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.542
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.526
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.467
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.597
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.068
# 반환된 coeff_elastic_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(elastic_alphas[0])
coeff_elastic_df.sort_values(by=sort_column, ascending=False)
alpha:0.07 alpha:0.1 alpha:0.5 alpha:1 alpha:3
RM 3.574162 3.414154 1.918419 0.938789 0.000000
CHAS 1.330724 0.979706 0.000000 0.000000 0.000000
RAD 0.278880 0.283443 0.300761 0.289299 0.146846
ZN 0.050107 0.050617 0.052878 0.052136 0.038268
B 0.010122 0.010067 0.009114 0.008320 0.007020
AGE -0.010116 -0.008276 0.007760 0.020348 0.043446
TAX -0.014522 -0.014814 -0.016046 -0.016218 -0.011417
INDUS -0.044855 -0.042719 -0.023252 -0.000000 -0.000000
CRIM -0.099468 -0.099213 -0.089070 -0.073577 -0.019058
NOX -0.175072 -0.000000 -0.000000 -0.000000 -0.000000
LSTAT -0.574822 -0.587702 -0.693861 -0.760457 -0.800368
PTRATIO -0.779498 -0.784725 -0.790969 -0.738672 -0.423065
DIS -1.189438 -1.173647 -0.975902 -0.725174 -0.031208
선형 회귀 모델을 위한 데이터 변환
print(y_target.shape)
plt.hist(y_target, bins=10)
# (506,)
(array([ 21., 55., 82., 154., 84., 41., 30., 8., 10., 21.]),
array([ 5. , 9.5, 14. , 18.5, 23. , 27.5, 32. , 36.5, 41. , 45.5, 50. ]),
<BarContainer object of 10 artists>)
from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures
# method는 표준 정규 분포 변환(Standard), 최대값/최소값 정규화(MinMax), 로그변환(Log) 결정
# p_degree는 다향식 특성을 추가할 때 적용. p_degree는 2이상 부여하지 않음.
def get_scaled_data(method='None', p_degree=None, input_data=None):
if method == 'Standard':
scaled_data = StandardScaler().fit_transform(input_data)
elif method == 'MinMax':
scaled_data = MinMaxScaler().fit_transform(input_data)
elif method == 'Log':
scaled_data = np.log1p(input_data)
else:
scaled_data = input_data
if p_degree != None:
scaled_data = PolynomialFeatures(degree=p_degree,
include_bias=False).fit_transform(scaled_data)
return scaled_data
# Ridge의 alpha값을 다르게 적용하고 다양한 데이터 변환방법에 따른 RMSE 추출.
alphas = [0.1, 1, 10, 100]
#변환 방법은 모두 6개, 원본 그대로, 표준정규분포, 표준정규분포+다항식 특성
# 최대/최소 정규화, 최대/최소 정규화+다항식 특성, 로그변환
scale_methods=[(None, None), ('Standard', None), ('Standard', 2),
('MinMax', None), ('MinMax', 2), ('Log', None)]
for scale_method in scale_methods:
X_data_scaled = get_scaled_data(method=scale_method[0], p_degree=scale_method[1],
input_data=X_data)
print('\n## 변환 유형:{0}, Polynomial Degree:{1}'.format(scale_method[0], scale_method[1]))
get_linear_reg_eval('Ridge', params=alphas, X_data_n=X_data_scaled,
y_target_n=y_target, verbose=False)
## 변환 유형:None, Polynomial Degree:None
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.788
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.653
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.518
alpha 100일 때 5 폴드 세트의 평균 RMSE: 5.330
## 변환 유형:Standard, Polynomial Degree:None
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.826
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.803
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.637
alpha 100일 때 5 폴드 세트의 평균 RMSE: 5.421
## 변환 유형:Standard, Polynomial Degree:2
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 8.827
alpha 1일 때 5 폴드 세트의 평균 RMSE: 6.871
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.485
alpha 100일 때 5 폴드 세트의 평균 RMSE: 4.634
## 변환 유형:MinMax, Polynomial Degree:None
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.764
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.465
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.754
alpha 100일 때 5 폴드 세트의 평균 RMSE: 7.635
## 변환 유형:MinMax, Polynomial Degree:2
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.298
alpha 1일 때 5 폴드 세트의 평균 RMSE: 4.323
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.185
alpha 100일 때 5 폴드 세트의 평균 RMSE: 6.538
## 변환 유형:Log, Polynomial Degree:None
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 4.770
alpha 1일 때 5 폴드 세트의 평균 RMSE: 4.676
alpha 10일 때 5 폴드 세트의 평균 RMSE: 4.836
alpha 100일 때 5 폴드 세트의 평균 RMSE: 6.241
X = np.arange(6).reshape(3, 2)
poly = PolynomialFeatures(3)
poly.fit_transform(X)
# array([[ 1., 0., 1., 0., 0., 1., 0., 0., 0., 1.],
# [ 1., 2., 3., 4., 6., 9., 8., 12., 18., 27.],
# [ 1., 4., 5., 16., 20., 25., 64., 80., 100., 125.]])
반응형
'Data_Science > ML_Perfect_Guide' 카테고리의 다른 글
| 5-6. 회귀트리 (0) | 2021.12.27 |
|---|---|
| 5-5. Logistics Regression (0) | 2021.12.27 |
| 5-3. Polynomial Regression, overfitting (0) | 2021.12.27 |
| 5-2. 보스턴 주택 가격 예측 || LinearRegression (0) | 2021.12.27 |
| 5-1. Gradient Descent (0) | 2021.12.27 |